Sub-blocking in BMS

Introduction

Sub-blocking allows selected blocks within a block model to be subdivided into smaller sub-blocks, each with its own values for each column. This allows finer resolution around areas of interest of the block model without drastically increasing the overall number of blocks within the block model. There are multiple sub-blocking methods available (fully sub-blocked, variable octree, and flexible), covering different use cases.

Sub-blocks are identified within parent blocks by one or more sub-block index columns, depending on the sub-blocking type. Each sub-block can be identified globally using either of the following:

• Index values (i, j, k) along with the sub-block index values (depending on sub-blocking method).
• Coordinate values (x, y, z) along with the individual block size (dx, dy, dz).

Index values (i, j, k) always refer to a parent block. The sub-block index columns refer to the sub-block within said parent block.

Coordinate values (x, y, z) can refer to the centroid of either a parent or sub-block, and (dx, dy, dz) denotes the size of the block around the centroid. When (dx, dy, dz) matches the model's parent block size, the centroid belongs to a parent block; and when (dx, dy, dz) is less than the parent block size, it is a sub-block.

When updating a sub-blocked model, you may choose to keep its existing geometry (changing only the values for each block), or to change its geometry. Changing the geometry of a model introduces some additional considerations.

Sub-blocking types supported

The Block Model API supports the following sub-blocking types:

• Fully sub-blocked
• Variable Octree
• Flexible

The type of sub-blocking must be the same over the entire block model and is selected upon creation of the block model, specified by the model_type field within the size_options object in the payload.

The value of this field can be either of the following:

• regular, for no sub-blocking.
• fully-sub-blocked
• variable-octree
• flexible

There is no way to change the base model_type of the block model after initial creation.

Fully sub-blocked models

For fully sub-blocked models, each parent block can be subdivided into a specified uniform grid, or left whole. The number of blocks within the sub-block grid is specified by the n_subblocks_per_parent field within the size_options object in the creation payload.

n sub-blocks per parent

The field n_subblocks_per_parent specified during model creation has the following allowed schema when creating a fully sub-blocked model, where nx, ny, nz can be integers between 1 and 100.

{
    "n_subblocks_per_parent": {
        "nx": int,
        "ny": int,
        "nz": int
    }
}

Variable octree models

For variable octree models, each parent block can be subdivided into a grid of sub-blocks, each of which can be potentially subdivided into its own grid of sub-blocks, and so on. This operation will be referred to as a split. Subsequent splits of sub-blocks can be applied a finite number of times. This limit of how many splits can be done is dependent on the block model field n_subblocks_per_parent.

n sub-blocks per parent

The field n_subblocks_per_parent specified during model creation has the following allowed schema when creating a variable octree model, where nx, ny, nz must be members of {1, 2, 4, 8, 16, 32, 64}.

{
    "n_subblocks_per_parent": {
        "nx": int,
        "ny": int,
        "nz": int
    }
}

The values assigned to each of nx, ny, nz represent the finest allowed resolution available to sub-blocks as a ratio of the parent block on the respective axis. That is, if we have nx = 2, ny = 4, nz = 8 then the finest resolution of a sub-block is $\frac{1}{2}$, $\frac{1}{4}$, and $\frac{1}{8}$ of a parent block in the $x$, $y$, and $z$ axes respectively.

Sub-blocking example

Say we have a variable octree block model with the following sub-blocking.

{
    "n_subblocks_per_parent": {
        "nx": 4,
        "ny": 8,
        "nz": 1
    }
}

Take any parent block and apply a split, it must be split in half along the $x$ and $y$ axes, resulting in the four sub-blocks shown below in Fig. 1; omitting the $z$ axis as nz = 1 (blocks cannot be split over the $z$ axis). This initial split is referred to as the first level of sub-blocking.

After the first split, the sub-block resolution is $\frac{1}{2}$ of a parent block in the $x$ and $y$ axes, meaning any of the sub-blocks shown in Fig. 1 can be split over both axes. Applying a split to the bottom right block along the $x$ and $y$ axes results in Fig. 2, referred to as the second level of sub-blocking. We now have a resolution in the $x$ axis of a $\frac{1}{4}$ of a parent block, and as such none of the sub-blocks created on the second level or higher can be split over the $x$ axis, as nx = 4.

Fig. 3 shows a split over the $y$ axis on every sub-block created in Fig. 2, referred to as the third level of sub-blocking. The sub-blocks created have a resolution of $\frac{1}{8}$ of a parent block, thus none of the sub-blocks created in the third level can be split over the $y$ axis.

Fig. 1 First level	Fig. 2 Second level	Fig. 3 Third level

Fig. 3 shows the highest resolution available for sub-blocks in this model. Note that multiple sub-blocks could have been split on the second level and subsequently on the third level.

As a general rule for variable octree models, each parent block can be subdivided over a combination of the $x, y, z$ axes into a grid of 2 (split over one axis), 4 (split over two axes), or 8 (split over all axes) sub-blocks. This subdivision can be reapplied to resultant sub-blocks, provided that the per-axis limits set by n_subblocks_per_parent are not exceeded. Additionally, if the max resolution of sub-blocks has not been reached for any axis, then it must be used when applying a split.

Flexible models

For flexible models, each parent block can contain one or more sub-blocks, each of which covers one or more cells within an underlying sub-block grid. The sub-block grid is a uniform grid of cells that covers the entire parent block, the number of cells within the sub-block grid is specified by the n_subblocks_per_parent field within the size_options object in the creation payload.

There are several other restrictions on sub-blocks within flexible models:

• Sub-blocks must be a rectangular prism in shape.
• Sub-blocks cannot overlap with any other sub-blocks.
• Sub-blocks must be fully contained within a single parent block.
• There cannot be any gaps between sub-blocks. When performing a geometry change update, you must provide all sub-blocks within a parent block, and thus they must cover the entire parent block.

n sub-blocks per parent

The field n_subblocks_per_parent specified during model creation has the following allowed schema when creating a flexible model.

{
    "n_subblocks_per_parent": {
        "nx": int,
        "ny": int,
        "nz": int
    }
}

where nx, ny, nz can be integers between 1 and 100.

Sub-block index

Sub-block index columns are used to identify sub-blocks within parent blocks.

Fully sub-blocked models

For fully sub-blocked models there is a single integer sub-block index column: sidx. When a parent block is not subdivided, the $sidx$ value is $0$, indicating the whole block.

To help understand the way $sidx$ is calculated for sub-blocks of parent blocks that are subdivided, imagine that the parent block is a regular block model with the following properties.

{
    "n_parent_blocks": {
        "nx": n_subblocks_per_parent["nx"],
        "ny": n_subblocks_per_parent["ny"],
        "nz": n_subblocks_per_parent["nz"],
    }
}

where indexing within the parent block follows the same convention used in regular models. So any sub-block within the parent block can be identified via $(s_i, s_j, s_k)$, where $s_i$ , $s_j$ , and $s_k$ are the indices of the sub-block within the sub-block grid. Rather than recording these three values as columns within the model, a unique $sidx$ is calculated for each.

For fully sub-blocked models, the $sidx$ of sub-blocks is calculated using: $sidx = 1 + s_i \cdot s_{ny} \cdot s_{nz} + s_j \cdot s_{nz} + s_k$

Where $s_{ny}$ and $s_{nz}$ are the number of blocks in the sub-block grid along the y and z axes respectively.

For example, say we have a parent block that has been fully sub-blocked using the following values.

{
    "n_subblocks_per_parent": {
        "nx": 2,
        "ny": 2,
        "nz": 2
    }
}

The parent block, viewed along the $z$ axis such that only the XY plane is visible, would look like the following:

In the figure above, the $sidx$ of each sub-block is shown in the center of the sub-blocks and $(s_i,s_j,s_k)$ is shown in the bottom-left. We can calculate $sidx$ of the bottom-right sub-block using the aforementioned formula to get the following:

$$\begin{matrix} sidx &=& 1 + s_i \cdot s_{ny} \cdot s_{nz} + s_j \cdot s_{nz} + s_k \\ &=& 1 + 1 \cdot 2 \cdot 2 + 0 \cdot 2 + 0 \\ &=& 5 \end{matrix}$$

Variable octree models

For variable octree models, there is a single integer sub-block index column called sidx. It is calculated and validated using pre-order tree traversal, where the parent block is root of the tree ($sidx$ = 0).

Earlier in the variable octree sub-blocking example, we showed a valid sub-blocking configuration of a parent block up to the third level of sub-blocking. Using the same n_subblocks_per_parent configuration as in the example gives the variable octree shown in Fig. 4 below, in which the children of nodes 14 and 27 have been omitted due to horizontal real estate limitations.

Fig. 4 Expanded variable octree

Each of the levels shown in the tree above represent the sub-blocking levels outlined in the variable octree sub-blocking example, where the root of the tree is considered level zero. Below is an example showing a similar sub-blocking as in Fig. 1, 2, 3, where the sub-blocking is applied to the bottom-left sub-block in Fig. 1 and sub-blocks are now indexed and coloured to show their placement on the tree in Fig. 8.

Fig. 5 First level	Fig. 6 Second level	Fig. 7 Third level

Fig. 8: Coloured expanded variable octree

Sub-blocks are spatially positioned such that if the child nodes under each level of sub-blocking were indexed similarly to how parent blocks are using $(i,j,k)$, the smallest index would map to the bottom left sub-block, and so on, incrementing along the $i$ axis, followed by the $j$, and finally the $k$ as shown below (omitting $k$).

Fig. 9 First level indexed	Fig. 10 Second level indexed

Flexible models

Unlike the other sub-blocking types, flexible models do not have a single sub-block index column, instead they have six index columns: start_si, start_sj, start_sk, end_si, end_sj, and end_sk. The columns start_si, start_sj, and start_sk are the indices of the first cell of the sub-block within the sub-block grid, and end_si, end_sj, and end_sk are the indices of the last cell of the sub-block within the sub-block grid.

These are the properties of the index columns:

• The start_s* and end_s* columns are inclusive, meaning that the first and last cells of the sub-block are included in the sub-block.
• The end_s* columns must always be greater than or equal to the start_s* columns.
• The start_s* and end_s* columns must be between 0 and n_subblocks_per_parent on their respective axis.

Updating sub-blocked models

Updating data in sub-blocked models has a different set of requirements than regular models.

When using the i, j, and k columns, you must also provide the sub-block index columns. On the other hand, when using x, y, and z columns, you must also provide the columns dx, dy, and dz.

In the initial update request, you must indicate whether the geometry of the sub-blocks will be changed. If the update will change the sub-blocking by creating or destroying sub-blocks, you must set the request field geometry_change to true, and provide all columns that are in the model. In this case, only new, update, and delete column operations are allowed as standalone operations. update_metadata is allowed, but only when the target columns are being updated as part of the update operation, and only when there are no columns being renamed. With regards to update type in this case:

• If set to "merge", then the sub-blocks provided inside the uploaded file must fully cover the parent blocks that are referenced in the same file. This is even if all the columns values for that sub-block are all null. This limitation can be disabled by enabling sub-block infilling.
• If set to "replace", then it is not required that the sub-blocks of a parent block fully cover the parent block. Upon querying the block model, then only the provided sub-blocks will be returned. Sub-blocking within parent blocks that are not provided in the file will be reset to a single un-subdivided block.

If the update does not change the sub-blocking, geometry_change can be omitted or set to false.

Sub-block infilling

By enabling sub-block infilling, you can upload a file containing only some sub-blocks for a given parent block (leaving some unspecified). In this case, when the previous version has a parent block and the uploaded file specifies some of its sub-blocks, the remaining sub-blocks are calculated in order to fill in the entire block. This functionality can be enabled for a given block model by setting the fill_subblocks field on the model, or overridden for a specific update with the fill_subblocks field on the update call.

To perform sub-block infilling:

• The model type must be fully sub-blocked or variable octree.
• Give each numeric column a unit (that isn't a length).
• Use an update with update_type set to merge, and geometry_change set to true.

Derived values depend on the column unit type:

• LENGTH returns a validation error because the value cannot be divided unambiguously.
• Absolute units of type MASS, VOLUME, and VALUE are divided in proportion to the volume represented by each derived block.
• Relative units of type MASS_PER_VOLUME, MASS_PER_MASS, VOLUME_PER_VOLUME, and VALUE_PER_MASS, plus ANGLE and CATEGORY, are copied to each derived block.

This process affects only sub-blocks not specified in the uploaded file. Infilled values depend on the previous parent block value, not the values in the uploaded file.

The infilling operation has two parts: a geometry update, which changes block geometry to accommodate the uploaded file, and a data update, which overlays the uploaded file values.

Fully sub-blocked infilling

For a fully sub-blocked model, infilling creates the missing sub-blocks needed to fill the parent block.

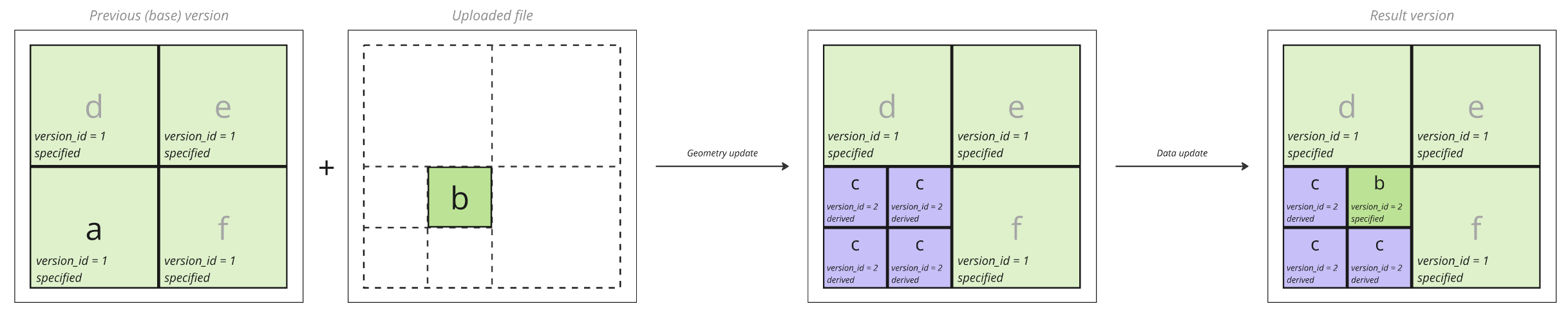Fig. 11: Fully sub-blocked infilling process. Here, a refers to the parent block value in the previous version; b refers to the uploaded sub-block value; and c refers to the derived value. Values d, e, and f refer to blocks not included in the uploaded file and remain identical after the update.

Infilled blocks are considered part of the resulting update, so their version_id is the result version ID even though the blocks were not directly included in the upload.

Variable octree infilling

For a variable octree model, the process is analogous to fully sub-blocked infilling. However, instead of completely subdividing and filling the entire parent block, it preserves the coarsest possible missing block within a parent sub-block tree branch.

A region whose finest leaves are all absent from the upload can therefore be represented by one larger derived octree block. Where a sibling is supplied, its missing sibling is retained as a smaller derived block instead. A result can consequently contain derived blocks at multiple octree depths within the same parent.

For example, if leaf sidx=5 is supplied and leaves in the other level-one branches are absent, the result can contain user-specified sidx=5, a leaf-derived sidx=6, and larger derived blocks such as sidx=1, sidx=7, and sidx=10. Consumers must not assume that octree infilling always returns the finest possible leaves.

In this example, the geometry update preserves supplied leaf sidx=5, derives its missing sibling sidx=6, and collapses fully absent branches into larger blocks sidx=1, sidx=7, and sidx=10. During the data update, derived absolute-unit values are scaled by block volume.

Subset of columns infilling

You can provide a subset of columns during a MERGE update with geometry_change set to true for both fully sub-blocked and variable octree model types. The operation fills missing columns for supplied blocks with data copied from the previous version when a matching sub-block already exists, or derives the values from the previous coarser block according to the sub-block infilling rules.

When the upload introduces coarser geometry than the existing geometry, the existing geometry is preserved and the uploaded block is subdivided to match it.

Sub-block derivation column

The sub_block_derivation system column identifies the source of the result:

Value	Meaning
user specified	The block geometry and all values were supplied by one or more updates.
derived from parent	The block geometry was generated by sub-block infilling and all its values were derived from the previous parent block.
some columns derived	One or more columns were derived from a previous version.

For a variable octree update containing only some finest leaves and only some columns, supplied leaves are reported as some columns derived; generated leaves and generated coarser blocks are reported as derived from parent. Query sub_block_derivation with the relevant columns to audit which results were supplied and which were inferred.

A null parent value remains null on the corresponding derived blocks.

The following example model has two columns: an absolute mass column, shown in grams, and a category column with high and low values. The uploaded file updates only the mass column; the category column is derived from the previous version for the supplied blocks.

Fig. 13: Column infilling example for a variable octree model, showing the interaction of column and sub-block infilling during merge updates.

Querying sub-blocked models

Querying data from sub-blocked models behaves like regular block models, see Querying block model data for details about the query workflow.

A few things specific to sub-blocked models:

• When doing a query where the geometry_columns field is set to "coordinates", additional columns: dx, dy, and dz will be included in the output file. These columns represent the size of each sub-block in the $x$, $y$, and $z$ axes respectively.
• When doing a query where the geometry_columns field is set to "indices", sub-block index columns will be included in the output file, in addition to the i, j, and k columns.
• XYZ bounding box selection is based on the parent block centroid locations. Currently, if a parent block's centroid is selected by the XYZ bounding box, then all sub-blocks will be included.